GRAFICZNA ILUSTRACJA

UKŁADU RÓWNAŃ

W tym rozdziale poznamy nową metodę rozwiązywania układów równań – metodę graficzną. W tym celu wykorzystamy informacje zebrane o układzie współrzędnych i funkcjach liniowych.

Rozważmy następujący układ równań:

Spróbujmy wyznaczyć z każdego równania niewiadomą y:

W otrzymanym układzie równań oba równania są wzorami funkcji liniowych. Każde z tych równań możemy przedstawić na układzie współrzędnych. Są to funkcje liniowe, więc wykresami tych wzorów będą pewne proste:

 

y

y

                              

 

 

 

                                                                      

 

 

 

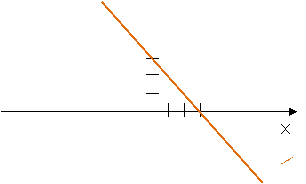
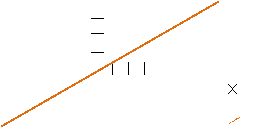
              Wykres funkcji y = -x + 3                                Wykres funkcji y = 0,5x

 

 

Możemy narysować obie te proste w jednym układzie współrzędnych:

 

 

 

 

 

 

 

 

                                                                                                    

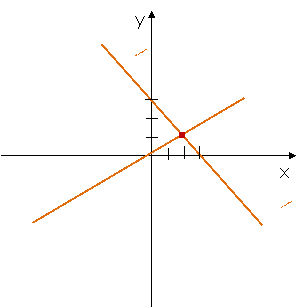
Zwróćmy uwagę na punkt przecięcia prostych. Punkt ten należy do obu prostych, więc jego współrzędne spełniają oba równania układu.

Współrzędne tego punktu (2,1) są rozwiązaniem układu równań:

Aby sprawdzić jej poprawność, wystarczy rozwiązać układ równań dowolną inną metodą (w naszym przykładzie będzie to metoda podstawiania):

Rozwiązanie naszego układu równań (x=2, y=1) odpowiada współrzędnym punktu przecięcia wykresów funkcji liniowych.

Należy pamiętać, że nie każde równanie pierwszego stopnia z dwiema niewiadomymi można przekształcić tak, aby otrzymać wzór funkcji liniowej. Na przykład po przekształceniu równania:

otrzymamy równanie:

… którego wykres funkcji jest równoległy do osi y.

Metoda graficzna nie zawsze jest skuteczna. Na układzie współrzędnych punkt przecięcia prostych może nie mieścić się na rysunku, bądź może być trudny do odczytania.

Warto zapamiętać, że jeżeli:

·        układ równań jest oznaczony (ma jedno rozwiązanie) to proste przecinają się w jednym punkcie,

·        układ równań jest sprzeczny (nie ma rozwiązań) to proste są równoległe do siebie,

·        układ równań jest nieoznaczony (ma nieskończenie wiele rozwiązań) to proste nakładają się na siebie i w konsekwencji otrzymamy tylko jedną prostą.